Nationale Wiskunde Dagen 2017
De 23e Nationale Wiskunde Dagen hebben plaatsgevonden op 3 en 4 februari 2017. Ga naar het archief voor o.a. handouts van de presentaties en foto's.
Hieronder staat het volledige programma van de NWD 2017 (het programmaboek is ook beschikbaar als PDF).
Programma
Openingslezing (vrijdag 11:30 - 12:30 uur)
Het Nederlandse volkslied of Wilhelmus is volgens het Guinness Book of Records het oudste volkslied ter wereld. Het is ontstaan tijdens de Nederlandse Opstand, een sleutelepisode in de geschiedenis van de Lage Landen. De dichter vereeuwigde in dit lied de tragische tweestrijd van de titelheld, Willem van Oranje: trouw blijven aan de Spaanse koning, of de ‘IJzeren hertog’ Alva verdrijven?
Het Wilhelmus is anoniem overgeleverd, waardoor er al eeuwenlang speculaties zijn over de identiteit van de auteur. Een Vlaams-Nederlands onderzoeksteam heeft het auteurschap van het Wilhelmus recent onderzocht met de computer. Dat gebeurde aan de hand van de stylometrie, waarin men de individuele schrijfstijl van auteurs aan de hand van wiskundige modellen tracht te vatten. Belangrijk is dat men daarbij niet zozeer kijkt naar opvallende stilistische kenmerken, maar vooral speurt naar minder opvallende patronen in de frequentie van kleine, weinigzeggende woordjes zoals 'ik', 'het' of 'maar'. Onze analyses wezen onveranderlijk in de richting van een onbekende, verguisde dichter die nooit eerder als kandidaat-auteur voor het Wilhelmus was genoemd: Petrus Datheen.
In deze lezing evalueren we de beschikbare historische gegevens over Datheen opnieuw. Het zal blijken dat deze dichter eigenlijk een uitstekende auteurskandidaat voor het Wilhelmus is. Centraal in deze discussie staat de spanning tussen kwalitatieve en kwantitatieve gegevens in wetenschappelijk onderzoek: hoeveel zeggingskracht hebben objectieve cijfers in een debat dat tot op heden vaak met subjectieve argumenten is gevoerd?
Blok 1 (vrijdag 14:00 – 14:45 uur)
Een bezoek aan de website http://www.mathcurve.com/courbes2d/courbes2d.shtml laat zien dat er ontzettend veel te vertellen valt over krommen. In deze lezing zullen we uit het enorme aanbod van krommen een tiental exemplaren kiezen. Alleen vlakke krommen komen aan de orde en we gebruiken hoofdzakelijk de kennis van elementaire meetkunde, toegelicht met behulp van plaatjes en animaties van GeoGebra-figuren. We laten ons leiden door onderlinge verbindingen tussen krommen.
In deze lezing beschouwen we drie typen van verbindingen, namelijk voetpuntskrommen, de roulettes – gegenereerd door langs elkaar rollende krommen – en ten slotte evoluten en involuten. Het idee van koppeling van twee krommen tot een paar van evolute en involute is afkomstig van Christiaan Huygens. We zullen dat bespreken in de geest van Huygens: met louter elementaire meetkunde en een beroep op de praktijk, namelijk inzicht in het rollen van een touwtje op een klosje. Hiëronymus van Alphen zei het al: ‘Mijn spelen is mijn leren, mijn leren is spelen.’
Sinds het begin van de Industriële Revolutie is vrijwel al het mechanische werk dat door mensenhanden gedaan werd, overgenomen door machines. Stoommachines konden krachtiger en efficiënter werken dan mensen, maar precisie ontbrak nog vaak. Er was geen manier bekend om perfect rechtlijnige bewegingen te maken zonder geleiders, die zelf perfect vlak moesten zijn. Alleen linkages, bestaande uit staven verbonden met scharnieren, kon men goed maken. Maak een pen vast aan een scharnier, en de linkage zal een figuur op papier zetten. Kunnen linkages dus een rechte lijn trekken, of is dit even onmogelijk als de driedeling van een hoek met passer en latje?
In deze lezing zullen we met behulp van computersimulaties verschillende linkages tegenkomen, ontworpen in de twee eeuwen sinds de Industriële Revolutie. Een linkage uit 1864 van Charles-Nicolas Peaucellier tekent inderdaad de perfecte rechte lijn. Met een aantal slimme constructies, een paar jaar later bedacht door Alfred Bray Kempe en uiteindelijk verstevigd door Abbot en Barton in 2009, is het zelfs mogelijk je handtekening te zetten met een linkage.
Interessante webpagina's
Gerard 't Hooft heeft drie verhandelingen geschreven over linkages van Meccano, op het niveau voor middelbare scholieren:
https://www.staff.science.uu.nl/~hooft101/lectures/meccano.pdf
https://www.staff.science.uu.nl/~hooft101/lectures/meccano2.pdf
https://www.staff.science.uu.nl/~hooft101/lectures/meccano3.pdf
Dat cirkels en parabolen zijn te geven door bijvoorbeeld de vergelijkingen x2 + y2 = 1 en y = x2, mag welbekend worden genoemd. Dit zijn voorbeelden van krommen in het vlak die je met vergelijkingen kunt geven. Gaan we een dimensie hoger dan krijgen we te maken met oppervlakken. Bijvoorbeeld x2 + y2 + z2 = 1 geeft een bol weer. Maar hoe ziet het oppervlak bij
(x2 + y2 – 6)(x2 + z2 – 6)(y2 + z2 – 6) = 1
er uit? Er is niemand die dit van tevoren kan zeggen. Daarvoor gebruiken we het gratis programma Surfer dat de kern vormt van een groot aantal posters van Imaginary. Het resultaat staat hierbij afgebeeld.

Door gebruik te maken van een paar eenvoudige basisprincipes is het mogelijk om vergelijkingen in elkaar te knutselen die oppervlakken van bijna elke gewenste vorm opleveren. Die basisprincipes zijn voor een wiskunde B-leerling goed te begrijpen en zo is Surfer een mooi middel om wiskunde B-stof tot leven te wekken.
Tijdens de voordracht zullen we een aantal van deze principes demonstreren. Voor degenen die zelf al wat willen proberen, Surfer is te downloaden van imaginary.org/program/surfer. Een voorloper van de tekst die voorbereid wordt, is te vinden op www.staff.science.uu.nl/~beuke106/Surferdemo.pdf
Bij het spelletje SET draait het om snelheid. Op tafel liggen twaalf kaarten en de spelers moeten zo snel mogelijk drie kaarten vinden die bij elkaar passen. Elke kaart heeft vier eigenschappen: kleur, vorm, aantal en vulling. Van elke eigenschap zijn er drie varianten. De kleur kan bijvoorbeeld rood, groen of paars zijn. Drie kaarten vormen een SET als ze per eigenschap alle drie dezelfde variant hebben of alle drie verschillend zijn.

Achter dit schijnbaar simpele spel blijkt een wereld van interessante combinatoriek schuil te gaan. Een paar voor de hand liggende vragen zijn: `Bevat een twaalftal kaarten altijd een SET?’ en `Hoeveel SETs kunnen er in twaalf kaarten zitten?’ (het voorbeeld in het plaatje heeft er zes).
In deze voordracht gaan we dieper in op de wiskunde achter SET en we bespreken de link met de recente onverwachte oplossing van een decennia oud probleem uit de combinatoriek.
Een meisje dat opgroeit met wiskundige formules als behang van haar kinderkamer, wat moet daarvan terecht komen? De Russische Sophia Vasilievna Kovalevskaya (1850-1891) leed een bijzonder leven met vele ups en downs. Ze was schrijfster, nihilist en bovenal wiskundige. Op achttienjarige leeftijd sloot ze een platonisch huwelijk om het land te kunnen verlaten en kwam ze terecht bij de Duitse wiskundige Karl Weierstrass, die zich over haar ontfermde.
In 1874 promoveerde ze summa cum laude aan de universiteit van Göttingen door maar liefst drie promotiewaardige artikelen aan te bieden. Eén van die artikelen bevatte het bewijs van wat we nu de stelling van Cauchy-Kovalevskaya noemen voor partiële differentiaalvergelijkingen. In 1883 pleegde haar man zelfmoord na diverse zakelijke tegenslagen.
Dankzij de inspanningen van bevriende wiskundige Gösta Mittag-Leffler werd Sophia een jaar later de tweede vrouwelijke universitaire wiskundehoogleraar ooit, na Maria Agnesi. In 1888 won ze de Prix Bordin voor haar werk aan de integreerbaarheid van de Kovalevskaya tol. Vanwege de kwaliteit van haar inzending besloot de jury zelfs het prijzengeld te verdubbelen. Ze heeft maar kort kunnen genieten van de roem die haar ten deel viel na het winnen van deze prijs, omdat ze in 1891 op eenenveertigjarige leeftijd bezweek aan een longontsteking. Na haar dood is ze door collega’s enerzijds geprezen en anderzijds verguisd, onder andere door een fout in een van haar wiskundige artikelen.
In de workshop staan we vooral stil bij Sophia’s grootste wiskundige prestaties: de stelling van Cauchy-Kovalevskaya en de Kovalevskaya-tol. We bekijken haar belangrijkste ideeën en hun relevantie voor de hedendaagse wiskunde. En de verleiding om er af en toe een smakelijke anekdote tussendoor te gooien zal zeker onweerstaanbaar zijn…
Er bestaat een aantal prachtige rekentrucs. Vooral als deze trucs gecombineerd worden heeft dat impact. Zelfs bij mijn ‘masterclass basisschoolleerlingen’: alle leerlingen wisten aan het eind van de sessie direct het antwoord van sommen zoals 1252 = …. en 106 x 108 = ….
Vooral het bewijs van dit soort rekentrucs is interessant, zowel meetkundig (voor basisschoolleerlingen) als algebraïsch (voor middelbareschoolleerlingen) . Sommige rekentrucs zijn samen te vatten met een verrassende generieke formule. Ook onderwerpen als de stelling van Pythagoras komen aan de orde.
Het is een workshop op de manier waarop ik jaarlijks mijn colleges Calculus op de VU begin. Met behulp van de nodige humor zullen de deelnemers na deze workshop een ruimere kijk op rekenen en algebra hebben.
Romanschrijvers die zich inlaten met onwrikbare wiskundige structuren? Wiskundigen die zich wagen in het onzekere domein van literaire verzinsels? Ze bestaan. Een inspirerend voorbeeld van kruisbestuiving tussen wiskunde en literatuur is de Oulipo, een in 1960 opgerichte, op mathematische leest geschoeide Franse werkgroep voor experimentele literatuur. De leden van de Oulipo (Ouvroir de Littérature Potentielle/Werkplaats voor Mogelijke Literatuur), stellen zich ten doel contraintes (strakke vormregels) te ontwerpen met behulp waarvan schrijvers het toeval uit hun werk kunnen bannen. Beperking bevrijdt, is hun stelregel. Beroepsmathematici zoals Claude Berge en Jacques Roubaud hebben daarvoor materiaal uit verschillende gebieden van de wiskunde aangedragen.
Een van de sterauteurs van de Oulipo, Georges Perec, ontleende de structuur voor zijn meesterwerk Het leven een gebruiksaanwijzing (La Vie mode d’emploi, 1978) onder meer aan een 10×10 Grieks-Latijns vierkant. In plaats van, zoals zijn mentor en mede-oprichter van de Oulipo Raymond Queneau het uitdrukte, ‘een willekeurig aantal personages als een troep ganzen nonchalant voor zich uit te drijven over een willekeurig aantal bladzijden of hoofdstukken’, vatte Perec honderden personages met hun levensverhalen in het raamwerk van een streng wiskundige patroon. En niet alleen zette hij het Parijse appartementengebouw dat een hoofdrol in zijn roman speelt in de steigers van een Grieks-Latijns vierkant, ook liet hij de volgorde waarin zijn personages ten tonele komen bepalen door de oplossing van een bekend schaakprobleem. Toch hield Perec zich niet altijd aan zijn eigen contraintes. Schijnbaar speelse ontregelingen gunnen de lezer een blik op de donkere bron van zijn schrijverschap.
Links: https://www.theguardian.com/books/booksblog/2013/jul/12/oulipo-freeing-literature-tightening-rules;
De meeste scholieren die hun vwo aan het afronden zijn en erover denken om hun opleiding aan een technische universiteit te vervolgen, verwachten dat uitvindingen die zij daar zullen doen een positieve invloed zullen hebben op belangrijke maatschappelijke zaken. Denk aan duurzame energie, schoon water voor iedereen, een veiliger samenleving, kwaliteit van leven, het doorgronden van het brein,en het vervaardigen van betere medicijnen. En hun verwachtingen zijn terecht. Ingenieurs dragen in belangrijke mate bij aan het oplossen van deze vraagstukken die ons allemaal aangaan.
In deze presentatie laat ik diverse aspecten van de wiskunde en natuurkunde zien die nodig zijn om tot een verbetering van bio-elektronische medicijnen te komen, waarmee ik de relevantie en noodzaak van deze wetenschappelijke talen aantoon. Op een voor een groot publiek behapbare manier komen de volgende onderwerpen aan bod: modellering, chips-technologie, halfgeleiderfysica, exponentiele functie, simplificatie, integraalrekenen, differentiaalvergelijking, fasoren, complexe getallen, schematuur, prototypering, co-design, metingen en interpretatie.
De presentatie geeft niet alleen inzicht in het wiskundig en natuurkundig gereedschap, maar ook in de toekomstige ontwikkeling van zogenaamde ‘elektroceutica’, die een grote impact zullen hebben op de toekomstige behandeling van neuronale aandoeningen zoals epilepsie, oorsuizen, verslavingen, migraine en chronische pijn.
Wanneer wiskunde in verband wordt gebracht met literatuur, gaat het standaard over vier onderwerpen:
- wiskundigen die ook een bijdrage hebben geleverd aan de literatuur;
- boeken waarin gesproken wordt over wiskunde;
- het feit dat in beide disciplines fantasie en creativiteit een belangrijke rol speelt;
- de relatie tussen taal en wiskunde.
Met het bovenstaande rijtje is niets mis. Maar we zouden er een element aan kunnen toevoegen: storytelling, het vertellen van verhalen. Want wanneer we wiskunde en storytelling combineren, ontluikt een nieuwe wereld. Ook wiskundedidactici hebben dat ontdekt, en sinds een jaar of tien wordt regelmatig over het onderwerp gepubliceerd.
Mensen vertellen elkaar dagelijks verhalen. Het vertellen van verhalen in de klas is misschien daarom zo gek nog niet. Bovendien, als je wiskunde ziet als een menselijke activiteit, als een belangrijk onderdeel van onze cultuur, dan kun je juist een brug slaan tussen de twee gebieden. Een les is eigenlijk ook een verhaal, net zoals een liedje, een beeld of een schilderij dat is. Maar waarover moeten die verhalen dan gaan? Is het überhaupt zinvol? Hoe kun je die inzetten in je les? Zijn begrippen uit de literatuurwetenschap geschikt om iets over de wiskundemethoden te zeggen, om je lessen nog beter te maken? Hoe kunnen we storytelling inzetten om leerlingen te motiveren?
Nadat ik eerst mijn best ga doen je te overtuigen, gaan we daarna zelf verhalen verzinnen en uitwisselen.
Zwaartekrachtsgolven zijn rimpelingen in de kromming van de ruimtetijd, waarvan Albert Einstein reeds honderd jaar geleden het bestaan voorspelde in het kader van zijn algemene relativiteitstheorie. Pas in 2015 zijn voor het eerst dergelijke rimpelingen waargenomen, wellicht afkomstig van samensmeltende dubbele zwarte gaten.
Naast het intrinsieke belang van deze ontdekkingen, brachten ze ons het tot dusver sterkste bewijs dat zwarte gaten überhaupt bestaan, en ze lieten toe om Einsteins theorie voor het eerst te testen in situaties waarbij de ruimtetijdkromming ontzettend sterk is en tegelijkertijd razendsnel verandert.
Tijdens de sessie beschrijf ik op een populariserende manier wat de aard is van zwaartekrachtsgolven, hoe ze zijn gedetecteerd en hoe de signalen verder zijn geanalyseerd. Daarnaast ga ik in op de verdere ontdekkingen die we in de komende jaren tot decennia kunnen verwachten in het pasgeboren vakgebied op de kruising van natuurkunde, astronomie, en kosmologie.
Landbouw ondergaat deze jaren een technologische revolutie: tractoren zijn rijdende supercomputers vol geavanceerde sensoren, dagelijks worden satellietbeelden van elk stukje aardoppervlak gemeten en opgeslagen, weersgegevens zijn per uur en per vierkante kilometer te verkrijgen... En dat is maar goed ook, want om de snel groeiende wereldbevolking te kunnen blijven voeden moeten we steeds efficiënter omspringen met de natuurlijke reserves.
De uitdaging is om al deze gegevens zodanig met elkaar te combineren dat dat ook lukt. Wiskunde en statistiek spelen hier een belangrijke rol in – een aantal voorbeelden zullen dit verduidelijken. Zo kan men aan de hand van gewasgroeimodellen, gebruik makend van bovengenoemde en andere gegevens, per perceel bepalen hoeveel mest nodig is om een optimale opbrengst te krijgen. Autonome robots zullen binnen afzienbare tijd in kassen rondrijden en met camera's de rijping van de tomaten vastleggen, wat weer kan leiden tot nauwkeurige schattingen van de hoeveelheid tomaten die over een paar dagen geoogst kunnen worden.
Ten slotte spelen big data zelfs een rol in het laboratorium: men kan, door het gedrag van luizen tijdens het voeden te bestuderen, inzicht krijgen in resistentie-eigenschappen van planten. Dit kan helpen in het ontwikkelen van nieuwe rassen die ecologisch vriendelijker te kweken zijn. De gebruikte wiskunde is zelf vaak vrij eenvoudig, maar bij het toepassen ervan komt heel wat ervaring en kennis kijken.
Op schalen van enkele tot honderden miljoenen lichtjaren blijken materie, sterrenstelsels en gas gegroepeerd in een karakteristiek webachtig patroon, het Kosmische Web. Volgens ons huidig inzicht moeten we het Kosmische Web zien als de transitiefase tussen de bijna uniforme materieverdeling in het vroege heelal en uiteindelijk volledig onder invloed van zwaartekracht in elkaar gestorte objecten zoals clusters en melkwegstelsels. Het kosmische web verschaft ons direct toegankelijke informatie over hoe de kleine dichtheidsfluctuaties in het vroege heelal worden vervormd door de werking van zwaartekracht.
Het ruimtelijke patroon van het Kosmische Web is uiterst complex. Het vormt een stochastische verdeling van structuren met een grote variatie aan morfologie en vorm, aan elkaar gekoppeld in een complex netwerk. We zien bovendien een grote verscheidenheid aan afmetingen, met kleine objecten ingebed in grotere structuren die zelf weer aaneen gesmeed zijn in nog weer grotere structuren. Dit laatste is een manifestatie van de hiërarchische wijze waarop structuur in het heelal is opgebouwd. Kleine objecten vormden zich in het vroege heelal, en smolten geleidelijk aan samen in steeds grotere configuraties en structuren.
Voor de beschrijving, analyse en modellering van de ingewikkelde kosmische patronen blijken geometrische en topologische concepten een centrale rol te spelen. Zij maken het mogelijk om de rijke verscheidenheid aan structuren zonder beperkingen te analyseren. In deze voordracht zal ik drie complementaire aspecten van de geometrische structuur en vorming van het Kosmische Web behandelen.
Kanker is een ziekte van het genoom. Soms erfelijk, maar vaker zorgen externe oorzaken, zoals roken, voor foutjes op het DNA. Hoe vroeger we die foutjes kunnen opsporen, hoe groter de kans op genezing. Maar wat zijn de essentiële foutjes op ons genoom van negen biljoen letters?
Moleculair biologen kunnen honderdduizenden (stukjes) genen meten en zo genetische profielen van tumoren vergelijken met die van gezond weefsel. Echter dit soort studies zijn qua patiëntenaantallen nog steeds vaak klein: variërend van, zeg, 50 tot 1000. Dit is dus big data van een speciale soort: veel gegevens van relatief weinig mensen, ofwel zogenaamde hoog-dimensionale data. De wiskundige uitdaging is om een robuuste, kleine set genomische markers te vinden die gezond en ziek weefsel onderscheiden, zodat relatief goedkope, objectieve diagnostische tests kunnen worden ontwikkeld.
Ik bespreek en visualiseer een tweetal populaire aanpassingen aan de gangbare kleinste kwadratenmethode, waarmee die toepasbaar wordt op hoog-dimensionale data. De data in de studie is echter niet de enige bron die we kunnen gebruiken. Er is tegenwoordig namelijk veel bekend over de genetische markers, en deze echte big data is systematisch opgeslagen in databases. Het zou zonde zijn om geen gebruik te maken van deze informatie. Ik leg daarom uit hoe we dat kunnen doen, en waarom dat uiteindelijk leidt tot betere markers. Als concreet voorbeeld ga ik in op genetische diagnostiek van baarmoederhalskanker, ter illustratie van hoe wiskunde kan helpen om betere markers te vinden met behulp van een test die comfortabeler is, omdat deze thuis is uit te voeren.
Blok 2 (vrijdag 15:30 – 17:00 uur)
Hoe teken je een kromme? Met je grafische rekenmachine, smartphone of laptop? Nee, natuurlijk niet! Al die dure apparaten! En uiteindelijk zie je daarmee een benadering waarvan de achterliggende wiskunde schimmig is. En ooit was er een wereld waarin deze hulpmiddelen niet eens bestonden...
In deze workshops gaan we old school. Met een latje, spijkertje, touwtje, plankje bouwen we machientjes om de mooiste krommen te tekenen. Ieder mechanisme legt bovendien een bijzondere eigenschap van die kromme bloot. We zullen niet nalaten een historisch perspectief aan te brengen. Vanaf de 17e eeuw stimuleerde het mechanisch denken namelijk de ontwikkeling van de analytische meetkunde.
Na een ritje naar de bouwmarkt organiseer je deze hands on-activiteiten voor je leerlingen eenvoudig op school en krijgen ze de analytische meetkunde letterlijk in de vingers.
Waarom wiskundigen niet mogen huilen, wanneer Cheryls verjaardag is en welke geheimen de Simpsons hebben: dat kunnen we allemaal ontdekken door de juiste boeken te lezen. Tegelijkertijd kunnen we ons verdiepen in wilde, grappige, grillige, geniale getallen, ervan genieten of er de anatomie van bestuderen. Verschijnselen als liefde, rijk worden en humor kunnen we ontdekken vanuit de wiskunde. En dan hebben we intrigerende fenomenen als magie, zoektochten, mysteries, telduivels en schandalen nog niet eens genoemd!
Er kan een wereld opengaan door een mooi boek. Maar kan het ook je wiskundelessen verrijken? Zijn er wiskundeklassiekers die in elke boekenkast zouden moeten staan?
Deze werkgroep is een ode aan de wiskunderoman, aan boeken die verhalen over de wiskunde en die ons inspireren en verwonderen. We gaan in op de vraag welke boeken je nu echt gelezen moet hebben als wiskundeleraar. De leeslijst die gebruikt wordt in de lerarenopleidingen van de NHL Hogeschool en de Hogeschool van Amsterdam onderwerpen we aan kritische blik, waarbij inbreng van de deelnemers wenselijk is. Daarnaast zullen we mooie lesactiviteiten delen rond gelezen boeken.
De workshop PQRS/(4Q), het vierde deel van puzzels, raadsels en spelletjes is een echte workshop. Je werkt anderhalf uur in tweetallen aan een afwisselende serie opdrachten. Je speelt spelletjes tegen elkaar, je maakt puzzels met apen en pionnen en nog veel meer andere dingen, en er is een keur aan raadsels om op te lossen.
Bij veel van deze onderdelen gebruik je concreet materiaal. Er is niet veel wiskundige voorkennis nodig; je zult wel vaak een oplossing vinden door gebruik te maken van wiskunde. Vereiste is een doortastende, frisse geest. De meeste opdrachten zijn ook zeer geschikt om in de klas te doen en de werkvorm is dat zeker ook. Aan het eind neem je een hand-out mee met alle opdrachten en krijg je ook de antwoorden.
Het is handig om passer, rekenmachine en liniaal bij je te hebben
Ook planten brengen ode aan de curves. In deze workshop voor zowel docenten onderbouw als bovenbouw, ontdek je hoe wiskundig allerlei bloemen en planten in elkaar zitten. Met echte planten op je tafel en liefst voorzien van je geodriehoek en grafische rekenmachine, leef je je helemaal in het leven van een bloem in. Waar zal je jouw volgende blaadjes laten groeien?
Je ervaringen als bloem proberen we wetenschappelijk en wiskundig te verklaren. Sommige historische wetenschappers waren je al voor: ook zij komen in deze workshop aan bod.
Deze workshop gaat over het aantal omwentelingen van draaiende schijven. Dit lijkt banaal, maar niets is minder waar. Voor verschillende onderlinge posities van schijven en afhankelijk van hun diameters gebeuren er onverwachte dingen. Wieldoppen bijvoorbeeld gedragen zich vreemd; keer op keer worden we misleid.
We kunnen in deze samenvatting natuurlijk niet verklappen wat er precies aan de hand is, want dan is de fun eraf tijdens de workshop. Het is de bedoeling dat de deelnemers de verschillende situaties in concrete voorbeelden onderzoeken en oplossen. We duiken daarna samen in de geschiedenis van de wiskunde: wieldoppen hebben namelijk alles te maken met de paradox van Aristoteles. Galilei heeft zich hier ook het hoofd over gebroken en een bijdrage geleverd aan de oplossing ervan. In de workshop wordt een hedendaagse oplossing uitgewerkt.
Tot slot onderzoeken we wat er aan de hand is met de snelheid van een wegschuivende ladder. U bent dus gewaarschuwd!
mathworld.wolfram.com/AristotlesWheelParadox.html
Symens, S. & Windels, B. (2008), Paradoxen in de wiskunde, Centrum voor Nascholing Onderwijs 2008-11-05
Om je wiskundelessen aan te laten sluiten op actuele ontwikkelingen in de wiskunde kun je bedrijven uit de directe omgeving betrekken bij je onderwijs in de klas. Dit maakt vakinhoud interessanter en geeft leerlingen meer zicht op beroepen binnen het vakgebied wiskunde en aangrenzende vakgebieden.
Maar als je dan ‘iets’ met bedrijven wil doen, wát ga je dan doen? Welk effect wil je bereiken? En hoe meet je het effect van de activiteit? Een excursie moet niet alleen leuk zijn, maar ook een bijdrage leveren aan de (wiskundige) ontwikkeling van leerlingen. In deze workshop komen dan ook niet alleen een aantal good practices langs, maar bespreken we ook hoe je het beoogde effect kunt meten en gaan we aan de slag om te kijken wat de volgende stap is in jouw samenwerking met het bedrijfsleven.
Bij studies als psychologie, biologie en diergeneeskunde is statistiek vaak een struikelblok. Een probleem is dat studenten hierdoor vaak te weinig op begripsniveau over statistiek kunnen redeneren.
Het Freudenthal Instituut wil leerlingen aan het eind van het voortgezet onderwijs de gelegenheid geven om zich een beeld te vormen van de statistiek op de universiteit en ze hier alvast wat ervaring mee op laten doen. Daartoe zijn acht online modules over statistiek ontwikkeld, waarin onderwerpen aan bod komen als beschrijvende statistiek, verdelingen, steekproeven en hypothesetoetsen met uitgebreide feedbackopties. De modules gaan specifiek in op statistisch begrip.
In de workshop krijgt u de gelegenheid met de modules te werken en mee te denken over mogelijke verbeteringen van de modules en van de aansluiting tussen statistiek in het voortgezet onderwijs en op de universiteit.
In islamitische regio’s, van Marokko via Egypte, Turkije tot in India, is een schat aan geometrische decoraties op gebouwen te vinden. De mozaïeken, vaak getuigend van groot vernuft, stammen uit een eeuwenoude ontwerptraditie. Het is verwonderlijk dat deze goudmijn nauwelijks is aangeboord in het wiskundeonderwijs.
In deze workshopsessie maakt u kennis met een tiental verschillende activiteiten om leerlingen actief aan de slag te laten gaan met allerlei wiskundige aspecten die aan de orde komen bij het construeren van geometrische patronen: spiegel- en draaisymmetrie, schuifsymmetrie, constructies met liniaal en passer of met vouwtechnieken, allerlei geometrische eigenschappen van lijnen, hun snijpunten, veelhoeken, een nieuwe kijk op het begrip ‘hoek’ die samenhangt met breuken, enzovoort. Deelnemers krijgen alle benodigde informatie om zelf in de klas deze activiteiten te organiseren, die variëren qua moeilijkheidsgraad van vmbo klas 1 tot vwo klas 5. Zie ook www.goossenkarssenberg.nl , www.patterninislamicart.com .
Verder zal een fascinerend eeuwenoud manuscript aan de orde komen. Dit manuscript licht een tipje van de sluier op over hoe men destijds te werk ging om de patronen te ontwerpen.
Er zijn van die lessen waarin het lijkt of leerlingen het idee hebben dat docenten hen alleen maar dwars zitten met moeilijke opgaven en bergen huiswerk, en docenten het idee hebben dat de leerlingen niet vooruit te branden zijn en dat ze het zo nooit gaan leren… Deze lessen zitten op slot, er wordt niet geleerd.
Een deel van het probleem (en daarmee de oplossing?!) ligt in de manier waarop wij als docenten naar onszelf kijken, hoe we naar de leerlingen kijken, welke verwachtingen wij van hen hebben én de verwachtingen en ideeën die de leerlingen over zichzelf hebben (Dweck, Boaler, Hattie). Ofwel: onze mindset.
Deze workshop gaat over de theorie van een ‘wiskundige mindset’. Wat is het? Wat betekent het voor de leerlingen? Hoe beïnvloedt hun én onze mindset hun leerproces? Om deze vragen te beantwoorden kijken we onder andere naar de mindset van de deelnemers aan de workshop. Vanuit de theorie van een wiskundige mindset zijn er een aantal strategieën toe te passen om een les in te richten vanuit een growth mindset. In een deel van de workshop werken we met bestaand lesmateriaal om dit concreet toe te passen.
In de workshop willen we laten ervaren hoe een andere aanpak van een les dan sommen uitleggen of bespreken kan leiden tot een leuke les.
Vaak is het een andere werkvorm, maar het kan ook zijn dat eerst concreet aan een probleem gewerkt wordt, zonder direct naar een antwoord toe te werken. De vraagstelling nodigt uit tot wiskundige denkactiviteiten. Op deze manier kan een gewone som uit het boek, die je op een andere manier brengt, tot een uitdagende lessituatie leiden.
Te denken valt aan :
- Vouwen van een rechthoekig blaadje (bijvoorbeeld een A4-tje), waardoor een driehoek ontstaat die varieert in oppervlakte.
Of een gevouwen posterlijst met variabele oppervlakte.
Of een gevouwen parallellogram. - Het ‘vouwen’ van een ellips of een hyperbool, en de betekenis van de vouwlijnen ontdekken.
- Van getekende lijnen naar een parabool.
Werkvormen als speeddaten, estafette, DUOotjes, pizzapunten, puzzelen enzovoorts zijn ook mooie manieren om afwisseling in je les te creëren. We geven daar in de workshop enkele voorbeelden van.
Sinds 1983 maak ik wiskunstige kerstkaarten voor leerlingen op de middelbare school en studenten aan de lerarenopleiding wiskunde. Vanaf 2006 koppel ik daar voor studenten een kerstprijsvraag (een soort praktische opdracht) aan vast, die uitdaagt tot het maken van een wiskunstig object of filmpje.
De kerstprijsvraag 2016 luidde: Ontwerp een kerst-/nieuwjaarskaart voor een (toekomstige) klas leerlingen, die voldoet aan zoveel mogelijk van de volgende ontwerpeisen:
- Het sluit aan bij wiskundeleerstof van het voortgezet onderwijs
- De ontvanger wordt aan het denken gezet
- Er zit een kunstzinnig element in
- Het activeert tot iets doen of iets maken
- Er is een prijsvraag aan verbonden
- Kerstelement in de vormgeving
- Een kerstgedachte
- Het jaartal van het nieuwe jaar
- Een wens voor het nieuwe jaar
- Originaliteit
In deze werkgroep bespreken we de voorbeelden uit mijn archief, de opbrengst van de kerstprijsvraag 2016 en het proces tot een ontwerp. Ik stel mijn archief ter beschikking en zet u aan tot creativiteit vanuit de leus: ‘creativiteit begint met jatten’.
Maak, enkel met pen en papier, een schets van de grafiek van y = 10-(4-x)4
Hoe schetsen we zelf, als docent, dergelijke grafieken met pen en papier? Welke kennis gebruiken we daarbij? Doen experts op dit gebied dit ook zo? En onze leerlingen in het voortgezet onderwijs? Is het nodig en nuttig om het schetsen van grafieken te onderwijzen aan leerlingen? En zo ja: hoe kunnen we dat dan effectief en efficiënt doen?
Al langer weten we dat enkel algebraïsche basisvaardigheden niet voldoende zijn om algebraïsche problemen op te lossen. Om algebraïsche basisvaardigheden functioneel te kunnen inzetten is symbol sense nodig: het strategisch kunnen werken met globaal kijken naar expressies en formules om de structuur te herkennen en om kwalitatief te redeneren.
Bij het schetsen van grafieken met pen en papier worden formules aan grafieken gekoppeld en komen veel van deze aspecten van symbol sense aan bod. Grafieken zijn meer toegankelijk voor leerlingen dan formules en geven in een oogopslag aan hoe de afhankelijke variabele afhangt van de onafhankelijke variabele. Hierdoor geven grafieken betekenis aan algebraïsche formules.
Onderzoek onder experts leverden ons een raamwerk op waarmee denkactiviteiten die bij het schetsen van grafieken een rol spelen, in beeld te brengen zijn. De (voorlopige) resultaten van dit onderzoek lijken ook voor andere terreinen van schoolalgebra van belang, zoals voor het oplossen van vergelijkingen.
In deze workshop werk je in groepjes van drie personen met allerlei materialen. Bij iedere opdracht kies je voorwerpen die een gevoel geven alsof je een spel gaat spelen. Bij de uitvoering van de opdrachten komen verrassende krommen tevoorschijn en ontstaat de behoefte aan wiskundige verklaringen.
Je kunt cirkels om andere cirkels of binnen andere cirkels laten draaien. Hoe beweegt een punt op de rand van een ronddraaiende cirkel? Als vanzelf ontstaan conflictlijnen tussen verschillende gebieden.
Schuin afgesneden cilinders leveren met papier en schaar verrassende krommen. Met knikkers kun je botsingen uitproberen tegen parabolische en ellipsvormige wanden. Verder kun je afwikkelkrommen van voorwerpen met verschillende vormen onderzoeken, of via het vouwen van papier krommen ontdekken. Ook zal het mogelijk zijn om met GeoGebra veel van de krommen te onderzoeken.
De meeste opdrachten zijn prima geschikt om met leerlingen te doen. Enige kennis over kegelsneden en elementaire goniometrische functies is handig bij de verklaringen.
Wij hopen je telkens te verbazen en kijken ernaar uit te zien hoe verwondering dwingt om verklaringen of formules te zoeken!
Voor deze workshop is het gewenst om een passer mee te nemen.
In deze sessie verkennen we twee problemen, namelijk de verdubbeling van de kubus en de driedeling van een hoek, waarvoor men sinds de klassieke oudheid naar een constructie met passer en liniaal heeft gezocht. Maar het bleek dat deze problemen niet met passer-en-liniaalconstructies op te lossen zíjn. Ze zijn dat wel als we één extra hulpmiddel toelaten: de neusisliniaal. Het gebruik hiervan ontsluit een deel van de wiskunde dat we met GeoGebra dynamisch kunnen verkennen.
We zien allereerst hoe een nieuwe klasse van krommen is te definiëren door gebruik te maken van een neusis- of inschuifmethode. Daarna passen we deze kennis toe om de geciteerde problemen op te lossen. Ook hierbij zullen we krommen ontmoeten die we niet met deze constructie identificeren.
We kijken eerst naar figuren in het platte vlak. We zien dat lijnen recht zijn en dat een cirkel gelijkmatig gekromd is. Gauss gebruikte de beweging van normalen om de kromming van figuren te bestuderen. We vragen ons af:
- Waar is de kromming positief en waar negatief?
- Kan je ook een kromming definiëren voor veelhoeken?
- Hoe staat het met het gemiddelde van de kromming?
Voor de cirkel en andere convexe figuren is het gemiddelde 2π. Wat zou die zijn voor de onderstaande figuren?

Voor rechtlijnige figuren is er een verband met de hoekensom.
Vervolgens stellen we dezelfde vragen voor oppervlakken in de ruimte. Voor de bol is de kromming constant en het gemiddelde is 4π. Wat kan je zeggen over de onderstaande figuren?

Voor de torus is het gemiddelde nul. Hoe zit dat? Kunnen we niet beter de absolute waarde van de kromming middelen? Wat komt er dan uit? En wat als de torus in de knoop zit? Wat is het effect van pukkeltjes op dat gemiddelde? En hoe ziet een ‘strak' oppervlak eruit?
Op deze en andere vragen hopen we tijdens de presentatie een antwoord te geven. We houden de redeneringen redelijk elementair en maken veel gebruik van figuren.
Als we YouTube als graadmeter nemen, dan lijkt het inzoomen in de Mandelbrotverzameling tot de populairste wiskundige activiteiten ter wereld te behoren. Zo heeft de clip Deepest Mandelbrot Set Zoom Animation ever meer dan twee miljoen views. Ook op de tentoonstelling Imaginary staat er een groot interactief scherm waarmee je kunt inzoomen op de Mandelbrotverzameling.
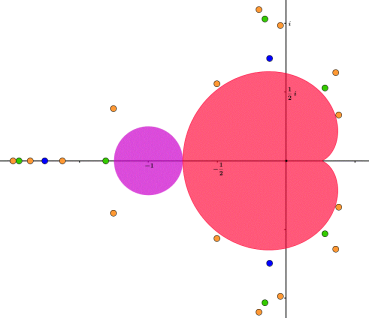
Maar wat zie je eigenlijk bij het inzoomen? En kun je hieraan rekenen met pen en papier? In deze werkgroep bepalen we de exacte plaats van de hoofcardioïde: het rode lijf van het appelmannetje in de figuur. Ook de positie van het paarse hoofd ernaast, de component van periode 2, berekenen we algebraïsch. Daarna gaan we op zoek naar de andere hyperbolische componenten en eindigen we in chaos.
Een elementaire kennis van complexe getallen is handig, maar liefhebbers van visuele pracht komen sowieso aan hun trekken. Verder laat de werkgroep zien dat GeoGebra ook voor dit onderwerp een fijn instrument is.
Werkvorm: combinatie van voordracht en zelf opgaven maken.
‘Hé, hoe is dat mogelijk?’, klinkt het door de zaal wanneer de goochelaar aan het werk is… een gevoel van verbazing en verwondering. Deze workshop is ontstaan uit een wisselwerking met professioneel goochelaar Herman Duffraing. Heel wat goocheltrucs steunen op wiskundige principes. Deze workshop wil een aanzet geven om te goochelen in de wiskundeles, als inleiding tot een wiskundig probleem.
We bieden een aantal goocheltrucs aan en tonen hoe je ze kunt inzetten in een wiskundeles. Het goochelen kan een teaser zijn voor de leerlingen, een motiverend element: hoe zit de truc in elkaar? Hoe werkt hij? Is er onderliggend een wiskundig model op te stellen dat de truc verklaart? Zonder een goochelaar te zijn, kan je met je leerlingen op zoek gaan, je leerlingen uitdagen en zo de magie breken die de goochelaar tot een bovenaards wezen verheft.
We leren enkele goocheltrucs aan en zoomen in op de wiskundige achtergrondinformatie. Na deze workshop kan je de volgende dag de klas instappen en je leerlingen verrassen met een uitdagende smaakmaker!
Technologie is constant in ontwikkeling, maar in de klassieke mechanica is weinig veranderd. Een mechanisch uurwerk heeft interessante techniek waarvan de oorsprong vaak in een ver verleden ligt. In hedendaagse horloges word volop gebruikt gemaakt van onder andere de Archimedesspiraal en cycloïden.
In deze lezing komt u meer te weten over de werking van een uurwerk en de herkomst van moderne uurwerktechniek. Het startpunt ligt bij de meetinstrumenten van professor Vening Meinesz, die hij gebruikte voor zijn beroemde Gravity expeditions at sea, in samenwerking met de Koninklijke Marine (zie ook de sessie van Bart Root).
Aansluitende workshop
Onder begeleiding van een professioneel horlogemaker werkt u in een aansluitende workshop aan een Zwitsers mechanisch uurwerk. Met behulp van diverse gereedschappen demonteert u zelf een gedeelte van het uurwerk en krijgt u inzicht in de toegepaste techniek.
In verband met de workshop: maximaal 20 deelnemers
Vening Meinesz expeditie: http://www.expeditiewikipedia.nl/#vening-meinesz
History of watchmaking: https://www.hautehorlogerie.org/en/encyclopaedia/history-of-watchmaking/
Gertjan Westerbeke: www.thejhc.nl; https://nl.linkedin.com/in/gertjan-westerbeke-b8a07465
Hoe je het ook probeert uit te leggen, goniometrie levert bij leerlingen problemen op. U kent ze vast: de overstap van goniometrische verhoudingen in (rechthoekige) driehoeken naar de definitie op de eenheidscirkel, de stap naar functies met de overgang van hoeken in graden naar hoeken in radialen, het gebruik van deze eenheidscirkel, …
In deze workshop gaan we in op een lessenserie die is ontworpen rond de reuzenraderen overal ter wereld. De een nog groter dan de ander. In de context van de reuzenraderen passeren allerlei vragen de revue die later simpelweg gekopieerd worden naar de eenheidscirkel. We starten vanuit de definities die leerlingen kennen uit de onderbouw.
De lessenserie, en ook deze workshop, begint met de geschiedenis van de reuzenraderen. De introductie leidt tot respect voor ingenieurs uit de 19e eeuw en de moderne tijd. We kijken ook nog even naar een ‘double Ferris Wheel’ waarbij mooie krommen opduiken die bij parametervoorstellingen weer gebruikt kunnen worden.
We lossen niet alle problemen met dit materiaal, maar door de goniometrie op een andere manier te introduceren, waarbij een groter beroep op eigen denkvermogen van de leerlingen wordt gedaan, creëren we een dieper begrip van de onderhavige materie bij leerlingen.
Leerlingenmateriaal, antwoorden en enkele proefwerkvragen krijgt u natuurlijk mee. U gaat naar huis met circa vier lessen, voor de bovenbouw (havo-)vwo.
Avondlezing (vrijdag 20:15 - 21:15 uur)
The experiments presented in this lecture combine two properties: On the one hand are they very easy to make, on the other hand they stimulate thinking and provide insight. These experiments cover many parts of mathematics: geometry, algebra, stochastics and work on rather different levels of mathematical pre-knowledge.
Vrijdagavondprogramma
Op vrijdagavond zijn er diverse actviteiten. U kunt een bezoek brengen aan verschillende tentoonstellingen: Mathematikum, linosneden van Henk van der vorst, en vrouwen in de wiskunde. De band dit jaar is Mosquito. Of doe mee aan de altijd spannende wisquiz, of daag uw collega's uit tijdens de spelletjesavond. Ook wordt er traditiegetrouw een aan wiskunde gerelateerde film vertoond.
Blok 3 (zaterdag 09:15 – 10:00 uur)
Aan de Universiteit Twente wordt in de vorm van een Lesson Study Team al jaren praktisch onderzoek gedaan naar didactische verbeteringen binnen het wiskundeonderwijs op de middelbare school. Verscheidene onderwerpen passeerden al de revue, waarbij de focus de laatste tijd lag op onderwerpen uit het nieuwe curriculum. In deze workshop presenteren we de bevindingen van twee onderwerpen: logaritmen en het inproduct.
Logaritmen komen in het nieuwe programma meer nadrukkelijk aan de orde bij Wiskunde A op het vwo, wat het des te belangrijker maakt om een goede basis te leggen. Leerlingen maken nogal eens rare fouten en begrijpen eigenlijk niet volledig wat ze aan het doen zijn. Is er misschien een andere aanpak mogelijk, meer gericht op intuïtie of eventueel voortbouwend op de geschiedenis?
Het inproduct komt op het vwo bij Wiskunde B om de hoek kijken en het blijkt nog niet zo eenvoudig om dit goed te introduceren. Pakken we nu de meetkundige definitie of beginnen we met de algebraïsche aanpak ? We bespreken nog een derde alternatief en doen verslag van onze ervaringen hiermee in de lespraktijk.
Emmy Noether (1882-1935) was misschien wel de wiskundige met de grootste invloed op de moderne natuurkunde, door haar ontdekking dat behoudswetten samenhangen met symmetrie. Ook was zij de ’moeder van de moderne algebra‘. In Moderne Algebra (ook de titel van het succesvolle boek dat Van de Waerden schreef op basis van de colleges van Noether in Göttingen) wordt niet veel gerekend, maar staan structuren abstract beschreven en hun eigenschappen uit de definities afgeleid. Zulke structuren zijn groepen, ringen, idealen, et cetera. Hierdoor ontstond een unificatie en vereenvoudiging van hele gebieden in de wiskunde, die hierdoor veel toegankelijker werden. Volgens de oude school was dit overigens geen wiskunde, maar theologie…
In deze lezing zullen we voorbeelden geven van hoe het bestaan van een behouden grootheid (zoals energie, impuls,…) in een mechanisch systeem samenhangt met een symmetrie in het systeem. Daarna kijken we naar de paradigma-verandering die Noether veroorzaakte in algebra rond het begin van de 20e eeuw. We kijken ook naar haar biografie, en de ontvangst van haar werk in het algemeen.
Voetnoot: de spreker is één van Emmy Noether’s 1218 wiskundige afstammelingen: zij is zijn betovergrootpromotor.
In 2014 kreeg Maryam Mirzarkhani de Fields-medaille – éénenvijftig mannen waren haar voorgegaan. Ze eerste vrouw met een Fields-medaille, gezien als de belangrijkste onderscheiding binnen de wiskunde, die eens in de vier jaar wordt uitgereikt aan een wislkundige jonger dan veertig jaar. Het was even wereldnieuws en omdat haar wiskundig werk zeer abstract is, had de internationale pers vooral aandacht voor het feit dat de Iraanse president twee foto's van haar twitterde: eentje mét en eentje zónder hoofddoek.
Deze uiterlijkheden zullen we verder laten voor wat ze zijn. Mirzakhani werkt aan de meetkunde en dynamica van hyperbolische ruimten. Maar wat is dat precies en welke resultaten heeft zij gevonden?
In drie beroemde komedies uit de wereldliteratuur wordt verwezen naar de kwadratuur van de cirkel: een echte komedie uit de Griekse oudheid, een komedie in verzen uit de late middeleeuwen en een komedie die een hoofdstuk is in een roman uit de twintigste eeuw.
Bij het klassieke probleem van de kwadratuur van de cirkel gaat het erom bij een gegeven cirkel met passer en liniaal een vierkant te construeren dat dezelfde oppervlakte heeft als de cirkel. De oude Griek onder de drie auteurs lijkt zo zijn twijfels te hebben aan de zinvolheid van dit probleem. De wiskundige, die hier de kwadratuur op het toneel wilde uitvoeren, brengt het er maar net levend vanaf.
De late middeleeuwer krijgt in deze voordracht veruit de meeste aandacht, omdat in zijn werk niet alleen de kwadratuur van de cirkel maar nog veel meer wis- en sterrenkunde een rol speelt. Bij hem is vooral het vermeend onoplosbare van het probleem van belang.
De moderne auteur is geboren in het jaar waarin de onmogelijkheid van de kwadratuur van de cirkel met passer en liniaal is bewezen. Hij lijkt dit geweten te hebben, maar er heeft een merkwaardige verdoezeling plaats met verdwenen jaartallen.
Symmetrieën van een gegeven figuur, functies en matrices zijn allemaal voorbeelden van de algemenere notie van een 'groep' en zelfs van een 'algebra'. In het eerste deel van de lezing zullen we deze twee abstractere noties invoeren, startend vanuit voorbeelden, en zullen we uitleggen waarom dit abstraheren nuttig is – zelfs als men geïnteresseerd is in concrete voorbeelden en problemen.
In het tweede deel komt een huidig onderwerp van onderzoek in 'geometric group theory' aan bod, namelijk 'de groei van een groep'. Alweer vertrekkend vanuit eenvoudige voorbeelden ontdekken we actuele onderzoeksvragen.
De veelzijdige kunstenaar Albrecht Dürer (1471-1528) schreef in de laatste paar jaren van zijn leven drie prachtig geïllustreerde studieboeken, waaronder Underweysing der Messung, een meetkundeboek bestemd voor beeldende kunstenaars. Het boek zou je kunnen vergelijken met een kunstexpositie verspreid over vier museumzalen (de hoofdstukken van het boek), elk met een eigen thema, waarbij de compilator niet alleen heeft verzameld en geordend, maar op een aantal plaatsen ook werk van zichzelf heeft uitgestald. De eerste drie zalen hebben als thema respectievelijk de eerste, tweede en derde dimensie. De vierde zaal bevat onder andere Dürers beroemde etsen waarin hij het perspectieftekenen uitlegt.
In mijn presentatie beperk ik me tot de eerste zaal, waarin allerhande kromme lijnen zijn tentoongesteld. Naast een diversiteit van spiralen en de drie klassieke kegelsneden is er onder meer ook een kromme te zien die nu met een beetje goede wil herkenbaar is als het ‘slakkenhuis van (Etienne) Pascal’, maar die eigenlijk naar Dürer had moeten worden vernoemd. Bij de rondleiding bekijken we ook mogelijkheden om de tentoongestelde krommen te koppelen aan stukjes wiskundeonderwijs.
De aarde en de andere planeten draaien in ellipsvormige banen rond de zon. Dit is één van de drie wetten van Kepler van het begin van de zeventiende eeuw. Op het einde van diezelfde eeuw heeft Newton aangetoond dat deze wet kan worden afgeleid uit zijn veel algemenere theorie over de gravitatiekracht en de wetten van de dynamica. Merkwaardig genoeg maakte Newton bij dit bewijs geen gebruik van `zijn' differentiaal- en integraalrekening, maar steunde hij enkel op `elementaire' meetkunde.
In 1964 gaf de beroemde fysicus Richard Feynman een lezing voor eerstejaarsstudenten waarin hij zijn eigen(zinnige) versie van dit bewijs van Newton presenteerde. Men dacht dat die lezing verloren was gegaan totdat dertig jaar later Feynmans voorbereidende schetsen en een bandje met de geluidsopname van de lezing opdoken. Het koppel Goodstein maakte er een boekje van.
Als je nooit echt begrepen hebt waarom de planeten ellipsvormige banen volgen, moet je ofwel dat boekje lezen, ofwel naar deze lezing komen. Met de steun van Kepler, Newton, Feynman en Goodstein leg ik het je het haarfijn uit, zonder één differentiaalvergelijking.
Bron: Goodstein, D.L., Goodstein, J.R. (1997). Feynman's lost lecture. The motion of the planets around the sun. Londen: Vintage.
Tijdens een studiereis naar Japan kwam ik in aanraking met Teaching Through Problem Solving (TTPS). Deze manier van wiskunde onderwijzen spreekt me aan omdat mijn indruk is dat TTPS enerzijds helpt om leerlingen wiskundige problemen te laten oplossen en het anderzijds bijdraagt aan een goed inzicht in wiskunde. De werkwijze heeft raakvlakken met Wiskundige Denkactiviteiten, maar een groot verschil is dat het probleemoplossen in Japan meer is geïntegreerd in het dagelijkse wiskundeonderwijs.

Op de foto staat het bord na afloop van een probleemoplos-les, waarbij het er om ging de oppervlakte te bepalen van de gele ‘citroen’ , zoals de leerlingen de figuur noemden – links op het bord. Op het mooie grote krijtbord (wie heeft die nog in het lokaal?) werden verschillende oplossingen genoteerd en besproken.
Het denken over probleemoplossen in het vak wiskunde is niet nieuw, zie bijvoorbeeld het werk van Duncker, Polya, Schoenfeld en Van Streun. Aan de andere kant: het rapport Onderwijs2032 ziet het versterken van het probleemoplossend vermogen als belangrijke vakoverstijgende vaardigheid voor de toekomst. Er is op dit gebied (nog steeds) werk aan de winkel. In deze workshop wil ik verkennen of en hoe de Japanse aanpak bruikbaar is in het Nederlandse wiskundeonderwijs.
Junior College, een initiatief van KU Leuven, biedt volledig uitgewerkte lespakketten van ongeveer twintig lesuren aan middelbare scholen. Het lesmateriaal vertrekt vanuit een motiverende toepassing (hier: de klimaatverandering) en bevat wiskundige leerstof die deels in de leerplannen vervat is en ze ook deels overstijgt. In het Junior College 'klimaatmodellering' worden differentiaalvergelijkingen aangebracht. We tonen aan dat klassieke (analytische) oplossingsmethodes vaak niet bruikbaar zijn en stappen daarom over naar een numerieke methode: de methode van Euler. Dit Junior College bevat daarnaast ook nog een inleiding op evenwichten en stabiliteitsanalyse en laat de leerlingen ook zelf een (zeer eenvoudig) wiskundig model opstellen voor oceaanstromen.
Het Junior College past in recente pogingen om de relevantie van wiskunde in de context van STEM (voor Science Technology Engineering and Mathematics) te verduidelijken, zonder aan diepgang in te boeten. De didactische aanpak is zeer interactief, met een sterke nadruk op zelfwerk, discussie en kritische reflectie. In deze voordracht gaan we zowel dieper in op de inhoud van dit Junior College als op de didactische aanpak.
In this workshop, we will work on a challenging task from the European project mascil. mascil – mathematics and science for life – aimed promoting inquiry-based learning (IBL) and the connection to the world of work (WoW). The process of Chocolate Bar Machine Scheduling was a fast and effective tool to involve students and teachers in a mascil learning environment and gives insight into mathematical ideas in operations research.
In the introduction phase of the task, the work place of a machine scheduler at a chocolate bar manufacturer is presented. For a customer order, five products have to be processed on two machines: on machine 1 the melted chocolate is poured into bars and on machine 2 the chocolate bars are packed. The processing time for each product on each machine is given. The job of a machine scheduler is to determine the order of the products such that the total processing time – the interval between the time the first product starts on machine 1 and the time the last product leaves machine 2 – is the shortest.
During the workshop you will work as a scheduler and try to find conditions for feasible solutions. After the work on the task and a plenary discussion on different approaches, we will discuss how to implement the lesson. This will be supported with experiences from Austrian teachers and some information about the mathematics underlying this task. The task will also be provided in Dutch to give you the opportunity to let your students work on it.
Het zijn fantastische, maar ook uitdagende tijden voor onderzoek in de sociale wetenschappen. Van dat wat deze wetenschapper nauw aan het hart ligt – bijvoorbeeld mens, land of bedrijf – kunnen we zowat alles meten. Naast traditionele data zoals sociaal-demografische indicatoren en vragenlijstgegevens, kunnen we gedrag op de sociale media registreren en is het zelfs mogelijk om het functioneren op het niveau van DNA of neuronen te meten. Dergelijk gegevens zijn bovendien dikwijls beschikbaar voor onderzoek, onder impuls van open data en open science-initiatieven. Hoewel deze gegevens aanleiding kunnen geven tot belangrijke nieuwe inzichten (bijvoorbeeld hoe school en ouders kunnen beschermen tegen een genetische aanleg tot criminaliteit), blijven de inzichten dikwijls uit en de data ongebruikt, of zijn de inzichten twijfelachtig of zelfs verkeerd (denk aan de val van de Google-flu-barometer en de hetze rond het ‘gay-gene’).
In deze presentatie gaan we in op de wiskunde en statistiek achter meten in de sociale wetenschappen en hoe deze wetenschap zich gedraagt en aangepast moet worden in de context van big data. We staan ook stil bij het fundamentele onderscheid tussen correlationeel en causaal onderzoek.
Om een idee over big data te krijgen verwijzen we graag naar volgende excellente presentaties: www.b2bnn.com/2015/05/the-top-3-ted-talks-on-big-data/
Neem ook een kijkje op: www.scientias.nl/mensen-facebook-account-leven-langer/
Er is geen voorkennis nodig; wel nodig ik de deelnemers uit om een vragenlijst in te vullen om de presentatie op eigen – uiteraard anonieme – gegevens toe te kunnen passen. Dus schrijf je je in voor deze sessie? Neem dan even contact op met k.vandeun@uvt.nl.
De opdrachten voor Wiskunde voor teams - de verzamelnaam voor de Wiskunde A-lympiade, de wiskunde B-dag en de OnderbouwWiskundeDag - worden ontworpen door de commissies die deze wedstrijden organiseren. Vanuit bij deze ontwerpervaringen organiseren we op de NWD een sessie waarin u onder begeleiding van commissieleden an de slag gaat met het didactiseren van onderwerpen van deze NWD. We proberen zo te komen tot een aantal (aanzetten voor) opdrachten vergelijkbaar met die voor Wiskunde voor teams.
Blok 4 (zaterdag 10:30 – 11:15 uur)
Hersenonderzoek staat sterk in de belangstelling. Zowel wetenschappelijke fascinatie als ook praktische uitdagingen liggen daaraan ten grondslag. De European Brain Council (www.braincouncil.eu) heeft enkele jaren geleden de economische kosten becijferd van hersenaandoeningen binnen Europa en kwam uit op een astronomisch bedrag van bijna 800 miljard euro over het jaar 2010. Deze kosten zullen door vergrijzing en leefstijl voorlopig alleen maar toenemen. Het is dus ook pure noodzaak om inzicht te verkrijgen in de bouw en de werking van ons brein, opdat we onze gezondheidszorg in de toekomst betaalbaar kunnen houden.
Hersenonderzoek vindt plaats op allerlei niveaus, vanuit velerlei disciplines en diverse invalshoeken. In mijn presentatie richt ik me op een praktisch aspect dat belangrijk is voor geneeskundige toepassingen, namelijk op de vraag hoe we de structuur van zenuwbanen in onze hersenen (het `wegennet’) in kaart kunnen brengen, uitgaande van wat we kunnen meten met klinische MRI-scanners. MRI staat voor `magnetic resonance imaging’, waarmee we de hersenen kunnen `doorlichten’.
In mijn presentatie zal ik het hebben over een relatief oude, maar klinisch vrijwel onbenutte mogelijkheid om met MRI de belangrijkste zenuwbanen af te beelden. De `I’ in MRI kan in dit geval beter gelezen worden als information, in de zin van verborgen, niet-visuele informatie, die slechts middels geavanceerde wiskundige technieken omgezet kan worden in bruikbare beelden. Ik zal tot slot een mogelijke toepassing ten behoeve van neurochirurgie laten zien.
sourceforge.net/projects/viste, het open source visualisatieplatform vIST/e.
Met fractalen in het vlak, zoals de verzameling van Mandelbrot, kan men mooie beelden genereren. Met nog een derde dimensie erbij gaat er een ganse nieuwe wereld open. Zo werden nog niet zo lang geleden driedimensionale fractale objecten ontdekt die men de Mandelbulb en de Mandelbox genoemd heeft. En er zijn nog een aantal andere, zoals objecten gebaseerd op zogenoemde Kleinse groepen.
In deze voordracht zal ik niet alleen hiervan vele mooie voorbeelden tonen, maar ook wat verder ingaan op de technieken die nodig zijn om die objecten op het computerscherm te toveren.
De Babyloniërs zijn bekend om het hoge niveau van hun sterrenkunde, die zowel precieze waarneming als voorspelling van astronomische fenomenen omvat. Rond 400 v.Chr. ontwikkelden ze wiskundige methoden om de schijnbare beweging van de planeten en de maan te berekenen.
Tot voor kort was men van opvatting dat ze daarvoor uitsluitend aritmetische methodes gebruikten. Dit is ontkracht door een ontdekking die in 2016 het tijdschrift Science haalde. Uit vier astronomische tabletten uit het British Museum te Londen, zeer waarschijnlijk afkomstig uit Babylon en “geschreven” tussen 350 en 50 v.Chr., blijkt dat Babylonische geleerden geometrische methodes gebruikten om de afstand te berekenen die Jupiter op zijn baan langs de hemel aflegt. Daartoe berekenden zij de oppervlakte van een figuur, die als grafische weergave van de variabele snelheid van Jupiter te interpreteren is. Wetenschapshistorici gingen er tot dan toe vanuit dat deze geometrische methode om de verplaatsing van een lichaam te berekenen, een voorloper van onze integraalrekening, in de 14e eeuw in Europa was uitgevonden…
Begin 1900 was het zwaartekrachtsveld van de aarde uitsluitend gemeten vanaf het land. Het klassieke enkel-slingerinstrument had namelijk een stabiele ondergrond nodig: onhaalbaar op schepen. Maar liefst 73 procent van het zwaartekrachtsveld op aarde was daarmee nog onbekend voor de geodetische gemeenschap.
Een jonge civiele ingenieur bracht daar verandering in: in 1915 kreeg de jonge doctor Felix Andries Vening Meinesz van de Rijkscommissie voor Graadmeting de taak om het eerste Nederlandse zwaartekracht-referentienetwerk op te zetten. Hij ontwierp speciaal hiervoor een slingerapparaat, ook wel ‘Het Gouden Kalf’ genoemd, dat het zwaartekrachtsveld met de hoogste nauwkeurigheid kon bepalen. Dit apparaat bleek zo effectief te zijn in het verwijderen van externe beweging, dat Vening Meinesz besloot het in onderzeeboten te gebruiken. Uiteindelijk opende dit de mogelijkheid voor oceanografisch zwaartekrachtonderzoek, wat leidde tot vele ontdekkingen die de theorie van plaattektoniek tot stand brachten.
Tijdens deze presentatie volgt u Vening Meinesz tijdens zijn expeditie van Den Helder tot Surabaya en leren hoe hij met zwaartekrachtsmetingen de vorm van de aarde bepaalde. Ook duiken we in de briljante wiskunde die hij gebruikte om het instrument te bouwen. Gaat u mee op avontuur?
De spreker heeft meegewerkt aan een historisch erfgoedproject dat de werken van professor Vening Meinesz aan boord van de onderzeeboot K-XVIII beschrijft. Enkele resultaten zijn te bekijken op de informatieve website http://expeditiewikipedia.nl/#vening-meinesz
Ruim 150 jaar geleden bracht de Engelse wiskundige Charles Lutwidge Dodgson (1832-1898) voor eigen rekening onder het pseudoniem Lewis Carroll het boek Alice's Adventures in Wonderland uit. Een paar jaar later gevolgd door Through the Looking-Glass and what Alice found there. In Nederland zijn deze boeken beter bekend als Alice in Wonderland en Alice in Spiegelland. Tegenwoordig betaal je voor een echte eerste Engelse druk van het eerste deel meer dan 1 miljoen dollar (!) en zijn beide boeken sinds die eerste uitgaven al die tijd onafgebroken in druk verkrijgbaar geweest. Bovendien is Wonderland in 174 verschillende talen uitgegeven en hebben meer dan 1200 verschillende illustratoren het boek verfraaid. (Wat is tenslotte het nut van een boek zonder plaatjes, vraagt Alice zich af).
In deze lezing hoop ik duidelijk te maken welke wiskundige, filosofische of logische aspecten bijgedragen hebben aan de populariteit van beide kinder(?)boeken. En in hoeverre de illustraties (van lieflijk via duister naar absurd) een belangrijke invloed hebben gehad op de populariteit van Alice. Wat was trouwens de invloed van de wiskundige Dodgson op de boekenschrijver Carroll? Ook zullen enkele aspecten uit Carrolls leven aan bod komen die hebben bijgedragen aan de verwonderlijke befaamdheid van onze heldin.
Ter voorbereiding: zie www.lewiscarrollgenootschap.nl.
Slotlezing (zaterdag 11:45 - 12:30 uur)
In this talk, we intend to address a few questions related to a big movie database, namely the Internet Movie Database (www.imdb.com). We will quickly describe the IMDb and use it to illustrate a few classical statistical tools introduced in high school (mean, median, least squares regression, etc.) This will allow us to emphasize some of the limitations of these standard methods and will give us the opportunity to introduce modern alternatives. Throughout, our focus is on the robustness of statistical methods, that is, on their ability to deal with atypical values in the database.

