Polyhedral Meshes
Discrete Surfaces in geometry processing and computer-aided design are commonly represented by triangle meshes. Triangles are popular since they are the simplest linear two-dimensional objects, trivially planar and readily suitable to finite-element formulations. Nevertheless, triangle meshes are disadvantageous in practice for several reasons: they have many edges, and consequently high vertex complexities, and they don't generally admit offset surfaces (it is impossible to build them with any “thickness”). In light of this, triangle meshes are unfavourable for fabrication and realization (construction). There is a growing interest in polygonal meshes, where every face is a non-triangular polygon. An important subclass is that of polyhedral meshes, where the polygons are planar. Polyhedral meshes can be realized with flat plates, such as glass or wood. Research in polyhedral meshes is thus mainly propelled by architectural and industrial design.

The challenge of working with polyhedral meshes is the inherent non-linearity and non-convexity of the planarity constraint. This makes the methodology of geometry processing for triangle meshes fairly complicated to generalize. Notable examples of methods in demand are remeshing, deformation, and analysis.

We focus on synthesis and deformation (editing) of polyhedral meshes. We compute polyhedral meshes in the popular subclasses of planar quad (PQ) and planar hex (PH) meshes, and devise general polyhedral patterns, following the well-known wallpaper tilings in the plane.
There are two relevant major challenges that we address: discovering the shapes that the tiles must assume in order to tile curved surfaces properly, and finding good orientation and sizing for the patterns on the surface.
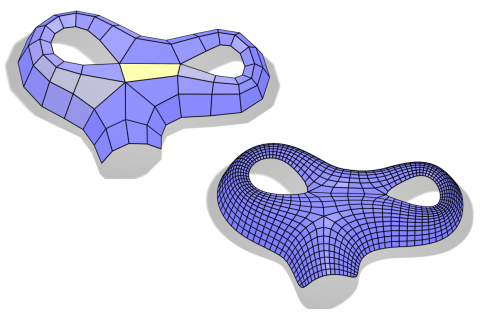
Editing given meshes into new ones, with the same connectivity, is a distinct challenge. We explore spaces of feasible transformations of meshes that maintain the planarity constraint. We research the important subclass of circular meshes, where every face is contained in a circumcircle. This brings about novel definitions of fairness and conformality, important in geometric analysis.
Additional details and video material can be found here.
| Caigui Jiang, Chengcheng Tang, Amir Vaxman, Peter Wonka, and Helmut Pottmann, Polyhedral Patterns. ACM Transactions on Graphics (Proc. SIGGRAPH ASIA), 34(6), 2015 |
| Amir Vaxman, Christian Müller, and Ofir Weber, Conformal Mesh Deformations with Möbius Transformations. ACM Transactions on Graphics (Proc. SIGGRAPH), 34(4), 2015 |
| Amir Vaxman and Mirela Ben-Chen, Dupin Meshing: A Parameterization Approach to Planar Hex-Dominant Meshing. Technical Report CS-2015-01 |
| Amir Vaxman, A Projective Framework for Polyhedral Mesh Modelling. Computer Graphics Forum 33(8), 2014 |
| Amir Vaxman, Modeling Polyhedral Meshes with Affine Maps. Computer Graphics Forum (Proc. SGP) 31(5), 2012 |
| Mirela Ben-Chen | Technion-IIT | |
| Caigui Jiang | KAUST | |
| Christian Müller | TU Wien | |
| Helmut Pottmann | TU Wien\KAUST | |
| Chengcheng Tang | KAUST | |
| Ofir Weber | Bar-Ilan University | |
| Peter Wonka | KAUST |

